Indexing Trees Revisited
2nd of April 2016After reading a white paper over at DZone about the benefits and consequences of the B-Tree structure, I decided to revisit the topic I already spent some thoughts on. The main argument for choosing B-Tree over other tree structures when designing your Key-Pair Value database, is that it enables optimal data retrieval performance (within the boundaries of the consequences I stipulated in the previous thought). However, the write performance takes a hit because of the structure, and thus it is selected when there is a significantly larger number of read over writes. However, when we consider the graphs below, it becomes evident that the performance of a B-Tree structure is mostly determined by the memory size afforded by the server it inhabits.
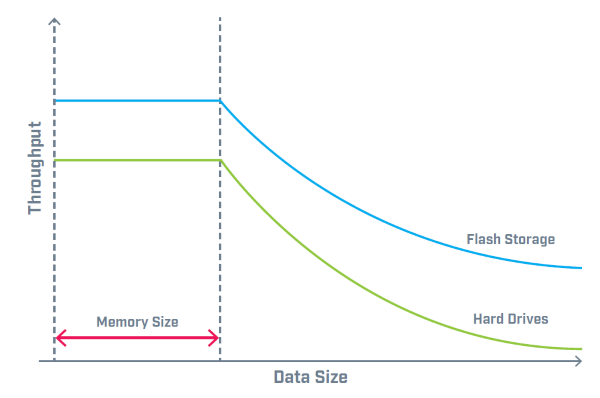
B-Tree structures are the most common index system used for NoSQL databases. Every B-tree is of some "order n", meaning nodes contain from n to 2n keys, and nodes are thereby always at least half full of keys. Keys are kept in sorted order within each node. A corresponding list of pointers is effectively interspersed between keys to indicate where to search for a key if it isn't in the current node. A node containing k keys always also contains k+1 pointers. So when we speak of an order 2 tree, this means 2 values and 3 pointers are set in each level (except of the lowest level, which is called a leaf node and contains only values). Thus when a value is searched, it is compared to the values of the root node. If not found, it determines which position the searched value would take in relation to the values contained in the node. If before all values, pointer 1 is followed to the next node. If in between, pointer 2 is followed, and if last, pointer 3 is followed. Same logic applies to writing new values to the database.
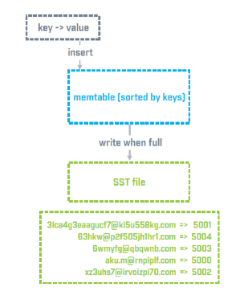
Log-Structured Memory Trees (LSM) work on the principle of storing incoming modification operations in a buffer (usually a memtable), and sorting/storing the data when the buffer has been filled up, transferred all data stored in the buffer in a single sequential operation. Each of these sequential operations creates an individual file. This indexing strategy has the advantage of a high update rate compared to the retrieval rate. This has the additional benefit of making a lookup in a single file fast, but renders a global search across all files slow. In order to tackle this drawback, database servers often employ maintenance logic to mitigate, such as file compaction (merging individual files), file levels (making file hierarchies) and the utilization of Bloom filters.
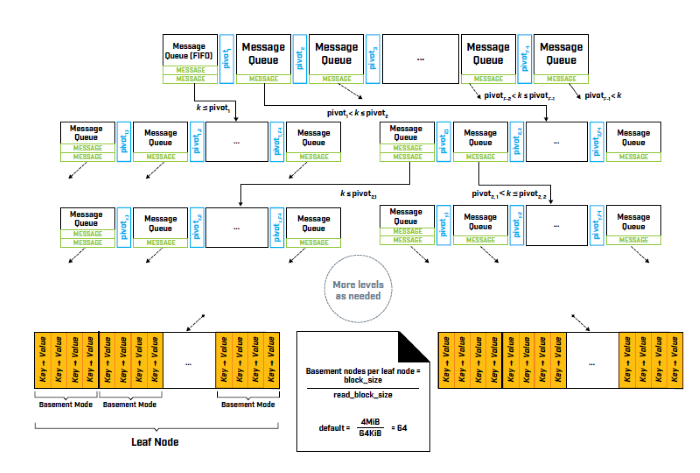
Fractal Trees are closer in structure to the B-tree variety. It combines the introduction of a buffer for applying changes with the tree structure of Balanced Tree Search structures. As the changes exceed the size of the buffer, they get pushed further down the tree. When the changes arrive at a leaf node, they get persisted within a single IO operation. With this approach, random operations are prevented from causing the performance degradation seen with LSM trees where data gets heavily modified. Data compression can further optimize performance. However, since there are a huge number of messages in a range of buffers, select statements must now traverse all the messages in order to find the needed result. As such, fractal trees are good for either databases with a lot of tables, a lot of indexes and a heavy write workload, or for databases with slow storage times.
Another way of improving performance of data retrieval is to optimize your search and aggregation algorithms. A popular way to do this in the Data Analytics realm is to employ the MapReduce algorithm. More on this algorithm in the following thought.
| Thought | EIM |